Research
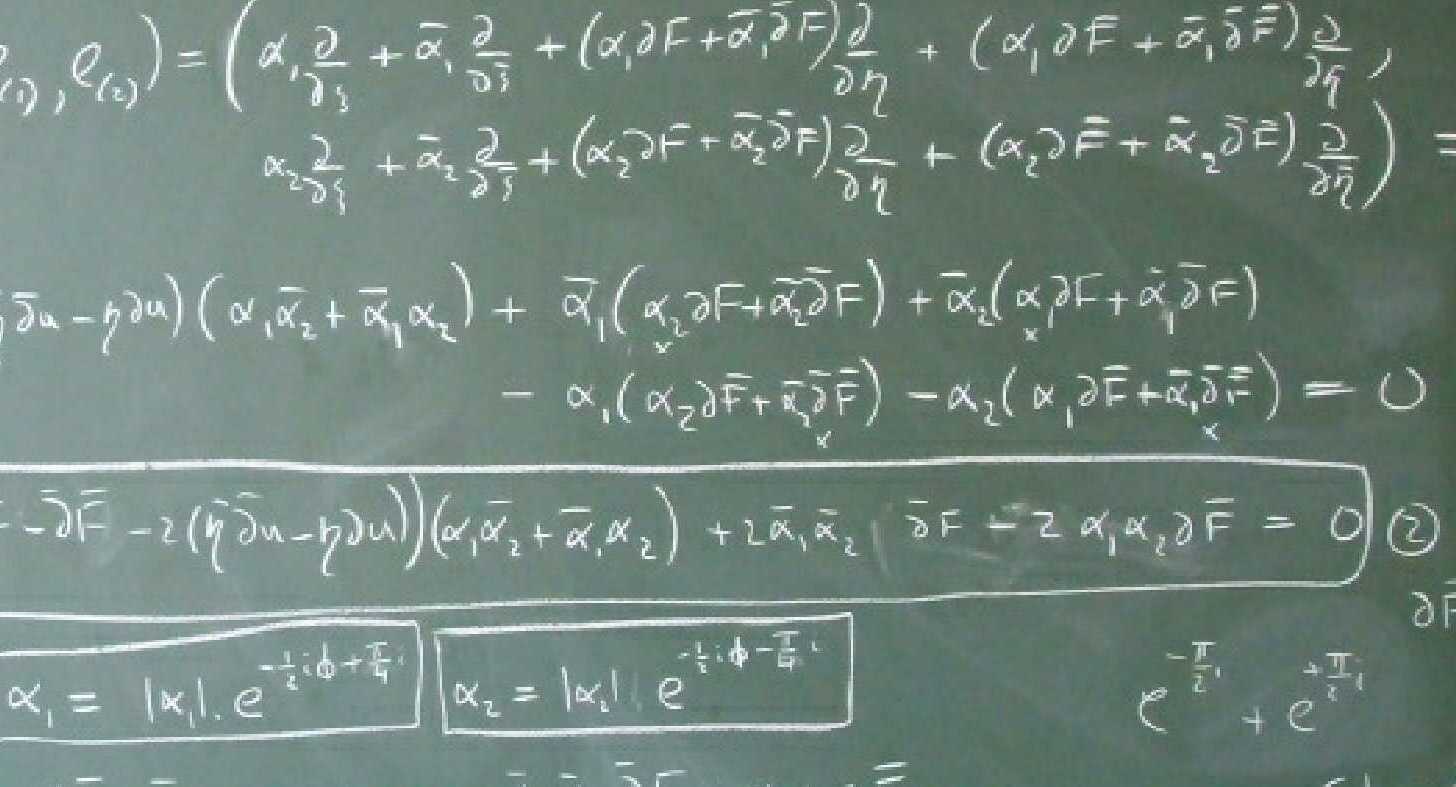 |
My main interests lies in differential and complex geometry of low dimensional manifolds. My first publications were in
general relativity and pseudohermitian 3-manifolds. In the latter, my aim was to apply the Newman-Penrose formalism from GR to
contact structures adapted to a Riemannian metric on a 3-manifold.
I became intrigued with the
complex structure on the space L of oriented affine lines of Euclidean 3-space. Together with Wilhelm Klingenberg, I discovered a
neutral Kaehler metric on the space L and have spent the last decade investigating the properties, applications and generalisations
of this structure. In this section I give a quick over-view of where this research has led. A mind-map of the topics is available here. |